Learning-Raytracing-in-8-weeks | Glass made out of voxels | Part 2
Intro
Hello, this is the second article of an 8 part series where I write down what I’ve learned about Raytracing on the CPU with voxels (which is of course in C++). I have used this template to which I have added features and refactored over the span of the 8 weeks. Here is the overview:
You can see the repo of my raytracer here.
Glass in a raytracer
A sphere of glass made out of voxels
Glass has been done many times in most real raytracers. You can even find a great explanation along with some code that does the trick from Peter Shirley’s well known tutorial, Ray Tracing in One Weekend.
Glass, or more generally a dialectric material has some interesting properties. Its behavior could be split into two parts: refraction and reflection.
Refraction in a cube of glass
I am going to start simple by only doing refraction. There is an equation that dictates what happens when light enters a medium that has a different index of refraction. Pure materials (or transparent) such as air, water, diamonds and glass interact with light based on their index of refraction, which I am going to call IOR from now on. The IOR defines a material. For instance, air has IOR of 1, water 1.3, glass 1.4 to 1.8 and so on. Computing a refracted ray is quite easy after you translate Snell’s law into code.
\[n_1 \sin(\theta_1) = n_2 \sin(\theta_2)\] \[\begin{align*} &\text{Legend:} \\ &- n_1: \text{Index of refraction of the medium the incident ray is traveling through.} \\ &- \theta_1: \text{Angle of incidence.} \\ &- n_2: \text{Index of refraction of the medium the refracted ray enters.} \\ &- \theta_2: \text{Angle of refraction.} \end{align*}\]This is still far from the down to earth float3 structs that we use to represent vectors in code, but deriving from the base formula we get this code:
1
2
3
4
5
6
7
8
//based on Raytracing in one Weekend
float3 Renderer::Refract(const float3 direction, const float3 normal, const float IORRatio)
{
const float cosTheta = min(dot(-direction, normal), 1.0f);
const float3 rPer = IORRatio * (direction + cosTheta * normal);
const float3 rPar = -sqrtf(fabsf(1.0f - sqrLength(rPer))) * normal;
return rPer + rPar;
}
I will skip the explanation of how to get there, as you can find it quite easily in Ray Tracing in One Weekend.
For further reading, I found an interesting course presentation that has a lot of good information on this topic.
How we traverse voxels
The algorithm I have in my project is based on this paper that describes the algorithm. The TLDR version is that when we shoot a ray, we check if it missed the whole voxel volume. If it did not, then we can increment the distance exactly to the next voxel until we get outside the voxel volume or hit a non-empty one.
This image is from a nice video explaining the traversal.
Some code at last
This is what we are going to do: 
Observe how the beam of light (purple) bends in the environment and then rotates to the same angle as it was before we got there. By using the other IOR ratio on the refracted ray inside we get the previos entering ray.
At the most basic, we need to refract in and out of the material, to do this, we need to figure out whether we are inside or outside the voxel. We are going to store that information in the ray and then assign the IOR ratio based on that. Like so:
1
2
3
4
5
6
7
//gets the color of glass if we are inside
float3 color{1};
//going to be set to true later
bool isInGlass = ray.isInsideGlass;
float IORMaterial = ray.GetRefractivity(mainScene); // defaults to 1.45
//get the IOR if the ray is inside or outside the glass
float refractionRatio = isInGlass ? IORMaterial : 1.0f / IORMaterial;
The angle of refraction is going to depend on the IOR ratio, which is the IOR of the environment we are going from (in this case, air 1.0) and the environment we are going in (glass 1.45).
Keeping track of where we are is quite simple at this point, as we can only refract into the glass voxel, and then refract again outside of the voxel. When we are inside of the glass, we need to get to the next non-glass voxel. That is what the “FindMaterialExit” method is doing.
1
2
3
4
5
6
7
if (isInGlass)
{
//add color of the glass, maybe expand with Beer Law
color = ray.GetAlbedo(mainScene);
//gets to the next non-glass voxel
mainScene.FindMaterialExit(ray, MaterialType::GLASS);
}
Normally, we would traverse the grid by just checking for a non-empty voxel. The modified version would look like this:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
bool Scene::FindMaterialExit(Ray& ray, MaterialType::MatType matType) const
{
// setup Amanatides & Woo grid traversal
DDAState s;
if (!Setup3DDDA(ray, s)) return false;
// start stepping
while (1)
{
const MaterialType::MatType cell = grid[s.X + s.Y * GRIDSIZE + s.Z * GRIDSIZE2];
//////////////////////////////////////////////////////////////////////////////////
// the conditional modifies the ray for the material type we pass //
//////////////////////////////////////////////////////////////////////////////////
if (cell != matType)
{
ray.t = s.t;
ray.indexMaterial = cell;
return true;
}
//////////////////////////////////////////////////////////////////////
// we just step through the grid as explained earlier //
//////////////////////////////////////////////////////////////////////
if (s.tmax.x < s.tmax.y)
{
if (s.tmax.x < s.tmax.z)
{
s.t = s.tmax.x, s.X += s.step.x;
if (s.X >= GRIDSIZE) break;
s.tmax.x += s.tdelta.x;
}
else
{
s.t = s.tmax.z, s.Z += s.step.z;
if (s.Z >= GRIDSIZE) break;
s.tmax.z += s.tdelta.z;
}
}
else
{
if (s.tmax.y < s.tmax.z)
{
s.t = s.tmax.y, s.Y += s.step.y;
if (s.Y >= GRIDSIZE) break;
s.tmax.y += s.tdelta.y;
}
else
{
s.t = s.tmax.z, s.Z += s.step.z;
if (s.Z >= GRIDSIZE) break;
s.tmax.z += s.tdelta.z;
}
}
}
return false;
}
To create a new ray, we compute a new direction for the refracted vector using the previous “Refract” method. For our origin, normally we would offset the intersection point by an epsilon value to avoid self-intersection. I found an article in Raytracing gems that does exactly that, but without using a parameter. It only uses the intersection point and the normal.
This is the intersection point we get when we call “ray.IntersectionPoint()”.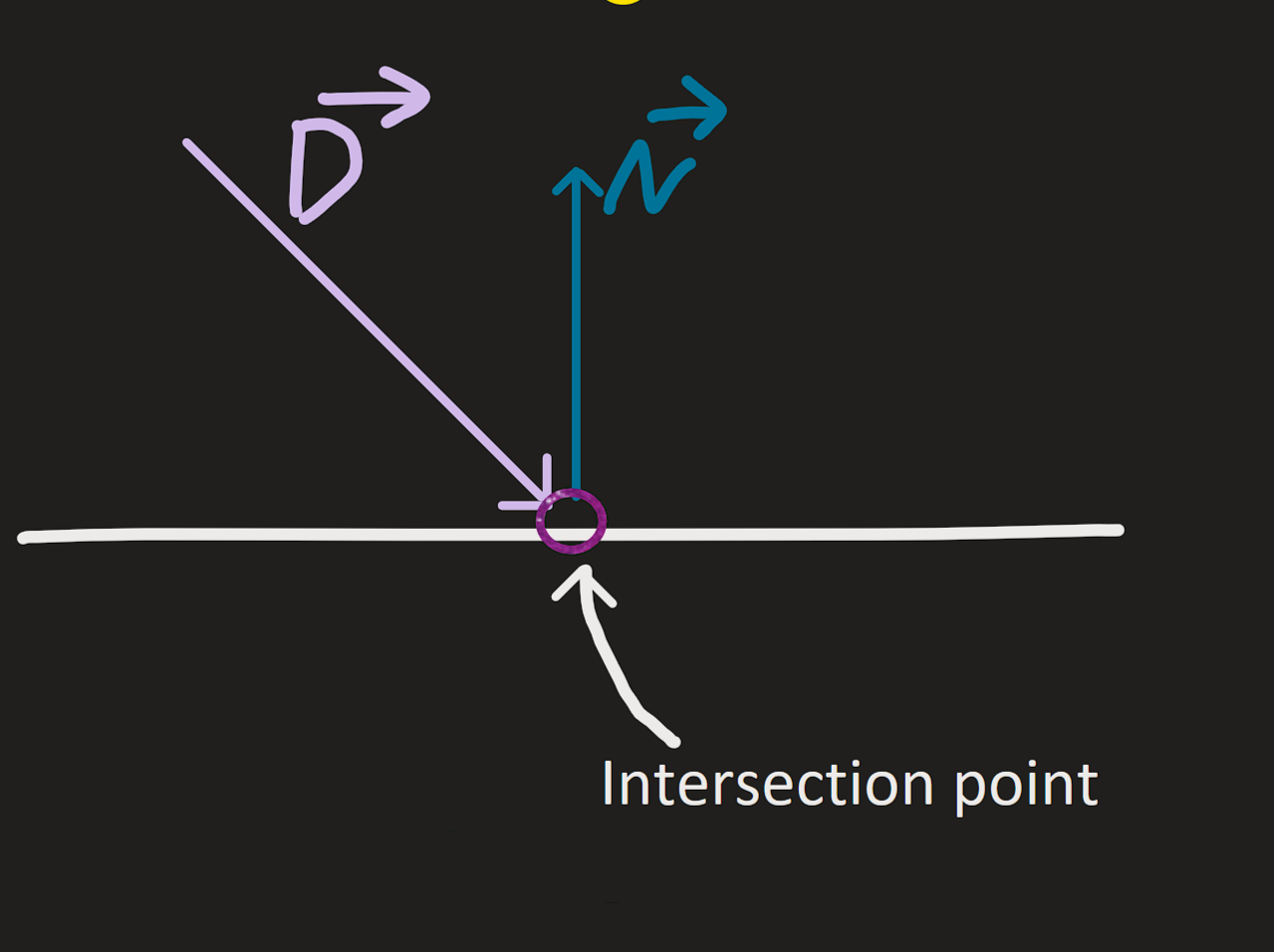 
When we call “OffsetRay” with a normal that is pointing outside the voxel.
When we call “OffsetRay” with a normal that is pointing inside the voxel.
All these vectors are unit vectors. Notice that when we are outside the glass, we want the next ray to start inside. However, when we are already inside the glass and we just hit the other side of the voxel, the next refracted ray will get a normal pointing towards the glass. Therefore, in that case, we also need a negative normal, so that the ray can start outside the glass. This is why we pass the negative normal, which will change when we can reflect inside or outside the glass (but for this implementation it will do fine).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
float3 resultingDirection = Refract(ray.D, ray.GetNormal(), refractionRatio);
//this is an implementation from Raytracing gems chapter 6: https://www.realtimerendering.com/raytracinggems/unofficial_RayTracingGems_v1.9.pdf
//this computes the origin of an ray assuring that it is not self-intersecting
float3 originDirection = OffsetRay(ray.IntersectionPoint(), -ray.GetNormal());
//we are exiting or entering the glass
isInGlass = !isInGlass;
//we need to create a new ray that starts a bit outside or inside the dialectric voxel
newRay = {originDirection, resultingDirection};
//set the booalean
newRay.isInsideGlass = isInGlass;
//continue the trace function
return Trace(newRay, depth - 1) * color;
The complete version we have so far.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
float3 color{1};
//code for glass
bool isInGlass = ray.isInsideGlass;
float IORMaterial = ray.GetRefractivity(mainScene); // defaults to 1.45
//get the IOR based if the ray is inside or outside the glass
float refractionRatio = isInGlass ? IORMaterial : 1.0f / IORMaterial;
//we need to get to the next voxel
if (isInGlass)
{
//add color of the glass, maybe expand with Beer Law
color = ray.GetAlbedo(mainScene);
//gets to the next non-glass voxel
mainScene.FindMaterialExit(ray, MaterialType::GLASS);
}
float3 resultingDirection = Refract(ray.D, normal, refractionRatio);
//this is an implementation from Raytracing gems chapter 6: https://www.realtimerendering.com/raytracinggems/unofficial_RayTracingGems_v1.9.pdf
//this computes the origin of an ray assuring that it is not self-intersecting
float3 originDirection = OffsetRay(ray.IntersectionPoint(), -normal);
//we are exiting or entering the glass
isInGlass = !isInGlass;
//we need to create a new ray that starts a bit outside or inside the dialectric voxel
newRay = {originDirection, resultingDirection};
newRay.isInsideGlass = isInGlass;
return Trace(newRay, depth - 1) * color;
And a render:
A refract only sphere of voxel
Getting reflections
In real life, glass also reflects light, so we would like our voxel sphere to also have that effect, like in this render:
Snell’s formula might have no solutions, which means we can’t refract at all.
\[n_1 \sin(\theta_1) - n_2 \sin(\theta_2) = 0\] \[\begin{align*} &\text{Legend:} \\ &- n_1: \text{Index of refraction of the medium the incident ray is traveling through.} \\ &- \theta_1: \text{Angle of incidence.} \\ &- n_2: \text{Index of refraction of the medium the refracted ray enters.} \\ &- \theta_2: \text{Angle of refraction.} \\ &- \text{No solution exists if } n_1 > n_2. \end{align*}\]Thus, we need to change our code (we will not always refract in and out of the material):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
float cosTheta = min(dot(-ray.D, ray.GetNormal()), 1.0f);
float sinTheta = sqrtf(1.0f - cosTheta * cosTheta);
bool cannotRefract = refractionRatio * sinTheta > 1.0;
float3 resultingDirection;
//this may be negative if we refract
float3 resultingNormal;
if (cannotRefract)
{
//reflect!
resultingDirection = Reflect(ray.D, normal);
//we do not change the boolean value
//isInGlass = !isInGlass;
//the normal used for the offset needs to point towards the same voxel we came from
resultingNormal = normal;
}
else
{
//we are exiting or entering the glass
resultingDirection = Refract(ray.D, normal, refractionRatio);
//we change the bolean value
isInGlass = !isInGlass;
//we keep the negative normal to offset correctly
resultingNormal = -normal;
}
newRay = {OffsetRay(ray.IntersectionPoint(), resultingNormal), resultingDirection};
newRay.isInsideGlass = isInGlass;
return Trace(newRay, depth - 1) * color;
What is important here is to keep track of where we are. If we reflect, we do not need to move the ray from the environment it is already in. If we are inside glass, we are just going to reflect inside it. If we are outside of it, we are still reflecting outside, so we do not need to change the “isInGlass” boolean.
With this change, we get reflection when refraction is impossible, which means at the edges: 
You could also add fresnel to your non-metal or metal materials for a bit more realism.
This does not quite look right yet, in real life you can see your reflection in a window. The Fresnel equation are desribing how much light gets into a material and how much it reflects.
Fresnel Equations:
For s-polarization: \(r_s = \frac{n_1 \cos(\theta_i) - n_2 \cos(\theta_t)}{n_1 \cos(\theta_i) + n_2 \cos(\theta_t)}\) \(t_s = \frac{2n_1 \cos(\theta_i)}{n_1 \cos(\theta_i) + n_2 \cos(\theta_t)}\)
For p-polarization: \(r_p = \frac{n_1 \cos(\theta_t) - n_2 \cos(\theta_i)}{n_1 \cos(\theta_t) + n_2 \cos(\theta_i)}\) \(t_p = \frac{2n_1 \cos(\theta_i)}{n_1 \cos(\theta_t) + n_2 \cos(\theta_i)}\)
As you can see, this is quite hard to read and to compute, this is why I am going to use the Schilick Approximation:
Schlick Approximation:
\[R = R_0 + (1 - R_0)(1 - \cos(\theta))^5\] \[\begin{align*} &\text{Legend:} \\ &- R: \text{Reflectance of the material.} \\ &- R_0: \text{Reflectance at normal incidence, given by } \left(\frac{n_1 - n_2}{n_1 + n_2}\right)^2. \\ &- \theta: \text{Angle of incidence.} \end{align*}\]Here is the code I am going to use:
1
2
3
4
5
6
7
8
//again from Ray Tracing in One Weekend
float Renderer::SchlickReflectance(const float cosine, const float indexOfRefraction)
{
// Use Schlick's approximation for reflectance.
auto r0 = (1 - indexOfRefraction) / (1 + indexOfRefraction);
r0 = r0 * r0;
return r0 + (1 - r0) * powf((1 - cosine), 5);
}
And now, we can add:
1
2
3
4
5
6
7
8
9
//other code
//RandomFloat has the range of [0 1].
if (cannotRefract || SchlickReflectance(cosTheta, refractionRatio) > RandomFloat())
{
//reflect!
}
else
//refract
We have already computed everything we need for the Schilick formula, we just need to plug the right parameters in and we are good to go.
One last render
Keep in mind that you can change the IOR of your material:
IOR of 1
A good rule of thumb is that an IOR of 1 should look like air (not taking into account the reflections).
IOR of 1.45
IOR of 2.4
A cornercase that you need to keep in mind is that when we get outside the voxel volume, we need to return the sky color. Here is the final version:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
{
float3 color{1};
//code for glass
bool isInGlass = ray.isInsideGlass;
float IORMaterial = ray.GetRefractivity(mainScene); //1.45
//get the IOR
float refractionRatio = isInGlass ? IORMaterial : 1.0f / IORMaterial;
bool isInsideVolume = true;
//we need to get to the next voxel
if (isInGlass)
{
color = ray.GetAlbedo(mainScene);
isInsideVolume = mainScene.FindMaterialExit(ray, MaterialType::GLASS);
}
//outside bounds
if (!isInsideVolume)
return skyDome.SampleSky(ray);
float cosTheta = min(dot(-ray.D, ray.GetNormal()), 1.0f);
float sinTheta = sqrtf(1.0f - cosTheta * cosTheta);
bool cannotRefract = refractionRatio * sinTheta > 1.0;
float3 resultingDirection;
//this may be negative if we refract
float3 resultingNormal;
if (cannotRefract || SchlickReflectance(cosTheta, refractionRatio) > RandomFloat())
{
//reflect!
resultingDirection = Reflect(ray.D, normal);
resultingNormal = normal;
}
else
{
//we are exiting or entering the glass
resultingDirection = Refract(ray.D, normal, refractionRatio);
isInGlass = !isInGlass;
resultingNormal = -normal;
}
newRay = {OffsetRay(ray.IntersectionPoint(), resultingNormal), resultingDirection};
newRay.isInsideGlass = isInGlass;
return Trace(newRay, depth - 1) * color;
}
Thanks for reading my article. If you have any feedback or questions, please feel free to share them in the comments or email me at bogdan.game.development@gmail.com.